Wir beschäftigen uns mal wieder mit einer lustigen Zahlenfolge, nämlich 1, 4, 16, 31, 65, ….? Niemand weiß genau, ob als Nächstes eine 99 oder doch eine 103 kommen soll. Die Folge beschreibt die maximale Anzahl an Singularitäten, also spitzen Punkten von Flächen vom Grad d. Ab Grad 7 ist die Anzahl unbekannt, aber die Weltrekordjagd hat interessante Flächen hervorgebracht, die aufgrund ihrer Singularität gar nicht leicht zu visualisieren sind. Das Programm SURFER kann es!
- SURFER (von Imaginary)
- SUSE Linux 7.1 Cover mit einer singulären Fläche (von Oliver Labs)
- Sendung mit der Maus: Glasfiguren durch Innengravur
- Mathe in Glas – Shop
- Überblicksartikel von Oliver Labs
- Paper von Breske, Labs, van Straten
- Folge A046001 in der OEIS



Feedback gerne auf Mastodon @Eigenraum@podcasts.social, an feedback (bei) eigenpod.de oder in die Kommentarspalte auf der Episodenseite.
Automatisch generiertes Transkript (nicht geprüft)
Hallo zusammen, willkommen im Eigenraum. Schön, dass ihr da seid.
Schön, dass ihr auf Play gedrückt habt oder zumindest nicht auf Stop gedrückt
habt, als der Algorithmus euch den Eigenraum auf die Ohren getan hat.
Ich will heute über Singularitäten reden. Und das ist nicht die KI-Singularität,
die, ja, im Silicon Valley vielleicht manche direkt vor der Haustür sehen.
Ich glaub da ja noch nicht so ganz dran, dass wir uns bald alle in Bunkern verstecken
müssen, weil die KIs die Weltherrschaft übernehmen wollen.
Hatte ich ja mit ChechiPT auch in einer früheren Folge, was war's,
18, glaub ich, drüber geredet.
Könnt ihr auch noch mal reinhören. in die KI-Folge.
So, dann wollte ich was sagen zu Spotify.
Es gibt einige neue Hörerinnen und Hörer auf Spotify. Das finde ich natürlich
immer toll, dass ihr mich da auch hört, aber ich will noch mal die Empfehlung
aussprechen, vielleicht doch auf eine richtige Podcast-App,
zum Beispiel Overcast auf dem iPhone, um zu satteln.
Denn da könnt ihr einige Features genießen, die auch in dieser Folge wieder
eine Rolle spielen werden.
Zum Beispiel Kapitelbilder, die bei Spotify noch nicht funktionieren.
Also die Kapitelmarken, dass man einzelne Teile der Folge anspringen kann.
Funktionieren ja jetzt mittlerweile bei Spotify, soweit ich das sehen kann.
Aber es gibt auch noch kleine Bildchen und ein Podcast-Player würde euch die
dann sozusagen anzeigen.
Aber Bildchen, die heute für diese Folge relevant sind, sind auch in den Shownotes
dann zu sehen, aber ich glaube auch Spotify würde diese Bilder nicht anschauen.
Die könntet ihr euch dann auf der Homepage eigenpod.de unter der Folgenseite noch anschauen.
Und was ich auch gesehen habe, Spotify hat jetzt Transkripte mit eingebaut.
Also es gibt jetzt auch direkt in Spotify ein Transkript. Das ist aber unabhängig
von meinem Transkript, was ich anbiete und wird noch mal komplett neu von Spotify
erstellt und mit, sagen wir mal, mangelhafter Technologie.
Also diese Spotify-Transkripte der Folge sind eine Katastrophe,
was ich bisher gesehen habe.
Und auch auf der Seite zu der Folge sind die von OpenAI Whisper erstellten Transkripte,
die ziemlich gut sind, wie ich finde.
Und wo auch die, wenn es mehrere SprecherInnen gibt, die SprecherInnen unterschieden werden und so weiter.
So, ich möchte euch heute eine Geschichte von Singularitäten erzählen und die
hat auch mit Polynomen zu tun und Flächen.
So, also Polynome kennt ihr ja vielleicht aus der Schule.
Die Polynomgleichung x² plus px plus q gleich 0 und um genau solche Polynome
und ähnliche Gleichung soll es heute gehen.
Und die Nullstellen von denen. Jetzt kennt man natürlich die Nullstellen von
einem Polynomen aus der Schule. Da berechnet man die mit der pq-Formel oder so.
Aber ich will jetzt Polynome in mehreren Variablen betrachten.
Die funktionieren aber genauso. Also wenn man ein Polynomen in zwei Variablen
hätte, x und sagen wir mal y oder x1 x2 irgendwie mehrere, dann kann man dann
eben die Quadrate davon bilden.
X² plus y² oder die miteinander multiplizieren x
mal y und man hat immer noch so einen
grad von einem polynomen das ist einfach der
höchste zusammengezählte exponent der davor kommt also so ein produkt x quadrat
hat den grad 2 aber x mal y hat auch den grad 2 im ein x und ein y haben und
wenn man sich jetzt die null stellen von so einem Polynom in zwei Variablen anschaut,
dann beschreibt das irgendwas in der Ebene.
Also man hat diese zwei Koordinaten, x und y, vielleicht im x-y-Koordinatensystem.
Und da wo das Polynom 0 ist, die 0-Stellen, ist irgendein Gebilde in der Ebene.
Und einer der Sätze der algebraischen Geometrie sagt, dass das eine Kurve ist.
Also die Lösungsmenge von einem Polynom, außer wenn das Polynom ein ganz spezielles
Polynom ist, ist im Allgemeinen, kann man davon ausgehen, dass das eine Kurve
ist, also etwas Eindimensionales.
Muss nicht unbedingt eine Gerade sein. Wenn es ein lineares Polynom ist,
kennt man es auch, da kriegt man eine Gerade, aber im Allgemeinen ist es eben
eine Kurve, die sich irgendwie winden kann und die kann sogar auch so Ecken haben.
Also wenn man eine Kurve beschreibt als Nullstellmenge eines Polynoms,
dann könnte die glatt sein, wie man sagt, also überall schön kontinuierlich
verlaufen oder sie könnte eine Singularität haben, eine Ecke.
Und ich will aber heute sogar über Flächen reden, also gehen wir noch eine Dimension höher.
Man nimmt jetzt ein Polynom in drei Variablen und die Lösungsmenge davon ist
auch wieder, also die Lösungsmenge von das Polynom ist 0, dieses Nullstellengebilde
des Polynoms, ist dann eine Fläche im dreidimensionalen.
Und dieser Satz, den ich eben schon erwähnt habe, der sagt eben,
dass eine zufällige Fläche immer schön glatt ist.
Also man könnte zum Beispiel an die Oberfläche einer Kugel denken.
Das ist ja die Lösungsmenge des Polynoms x² plus y² plus z² ist gleich r² für
irgendein r, sagen wir mal 1.
Wenn ich das als Nullstellengebilde von einem Polynom schreiben will,
nehme ich einfach x² plus y² plus z² minus 1 ist gleich 0.
Ich bringe einfach die minus 1 auf die andere Seite. Und dann habe ich die Oberfläche der Kugel.
Alle Punkte, die auf der Oberfläche der Kugel liegen, bilden eine schöne glatte Fläche.
So, aber wenn ich jetzt zum Beispiel x² plus y² minus z² gleich 0,
setze, dann bekomme ich einen doppelten Kreiskegel Also stellt euch mal so einen
Kreiskegel vor, wie so eine Zuckertüte und an der Spitze ist aber jetzt noch eine Zuckertüte,
die in die andere Richtung nach unten geöffnet ist.
Und das ist die Lösungsmenge von dem Polynom, was ich eben gesagt habe,
wo ich x² plus y² minus z² gleich 0 gesetzt habe.
Und wenn man sich jetzt mal überlegen würde, dass man das versucht irgendwie 3d
zu drucken oder so sieht man sofort dass
man da an der spitze ein problem
hat das wird nicht sehr stabil sein und das
ist so eine typische singularität also singularität
ist irgendwie ein punkt an dem
die fläche sich nicht wie eine fläche verhält weil die sich so
zusammenzieht wie an der spitze der zuckertüte und
dort einen punkt ausbildet der irgendwie wo
der dimensionsbegriff vielleicht nicht mehr so ganz passt also wo es eben
keine fläche ist wo mehrere linien die auf der
fläche verlaufen unabhängig verlaufen auf einmal zusammen
kommen so jetzt ist es so dass man wenn man
ein zufälliges polynom nimmt dann ist das immer glatt aber es gibt spezielle
polynome bei denen diese singularitäten auftauchen und verschiedene polynome
unterscheidet man anhand ihrer koeffizienten also der zahlen und vorzeichen
die davor den x quadrat plus y quadrat gehen und anhand des.
Also die beiden, die ich jetzt gerade benutzt habe für die Kugel und den Kegel,
das waren eben Polynome vom Grad 2.
Wie die Menschen immer so sind, oder die MathematikerInnen, dann fragen sie
sich natürlich, kann ich das total singulär machen, wie viele von diesen Singularitäten
kann ich eigentlich in so eine Fläche einbauen?
Und darum soll es heute gehen.
Es gibt eben diese schwer zu findenden, speziellen Flächen, die isolierte Singularitäten
haben. Und das ist eigentlich schon so ein bisschen Mathematik aus dem 19.
Jahrhundert, Mitte des 19.
Jahrhunderts fängt das an, dass man sich damit beschäftigt, wie viele solche,
Singularitäten kann man eigentlich haben.
Und es ist schon lange bekannt, dass so eine quadratische Fläche,
also eine, die durch ein quadratisches Polynom beschrieben wird,
nur eine Singularität haben kann.
Also dieser doppelte Kegel ist das einzige Beispiel.
Es gibt natürlich noch andere wie verformte Kegel oder so, aber diese Art der
Singularität und die Anzahl der Singularitäten bei einer durch ein quadratisches
Polynom beschriebenen Fläche ist immer höchstens 1.
Also es gibt die glatten Flächen, die keine solchen Singularitäten haben und die, die eine haben.
Eigentlich könnte man sogar bei Grad 1 anfangen. Also wenn man eine Fläche durch
ein Polynom von Grad 1 beschreibt, dann ist das ein lineares Polynom und die
Fläche ist einfach eine Ebene.
Die hat gar keine Singularitäten.
Und vielleicht seht ihr jetzt schon, wie der Hase läuft. Man erhöht jetzt den
Grad und fragt sich, kann ich die Fläche oder eine Fläche finden,
die die maximale Anzahl von solchen isolierten Singularitäten hat.
Und da kommen ganz schöne Flächen dabei heraus. Und wenn ihr jetzt einen Podcastplayer
mit Kapitelbildern habt, dann seht ihr ein paar von diesen Flächen,
über die ich jetzt gleich rede, in eurem Podcast Player.
Und wenn nicht, dann müsst ihr einmal auf der Homepage oder auf unserem Social
Media Kanal auf Mastodon vorbeischauen. Da könnt ihr die auch sehen.
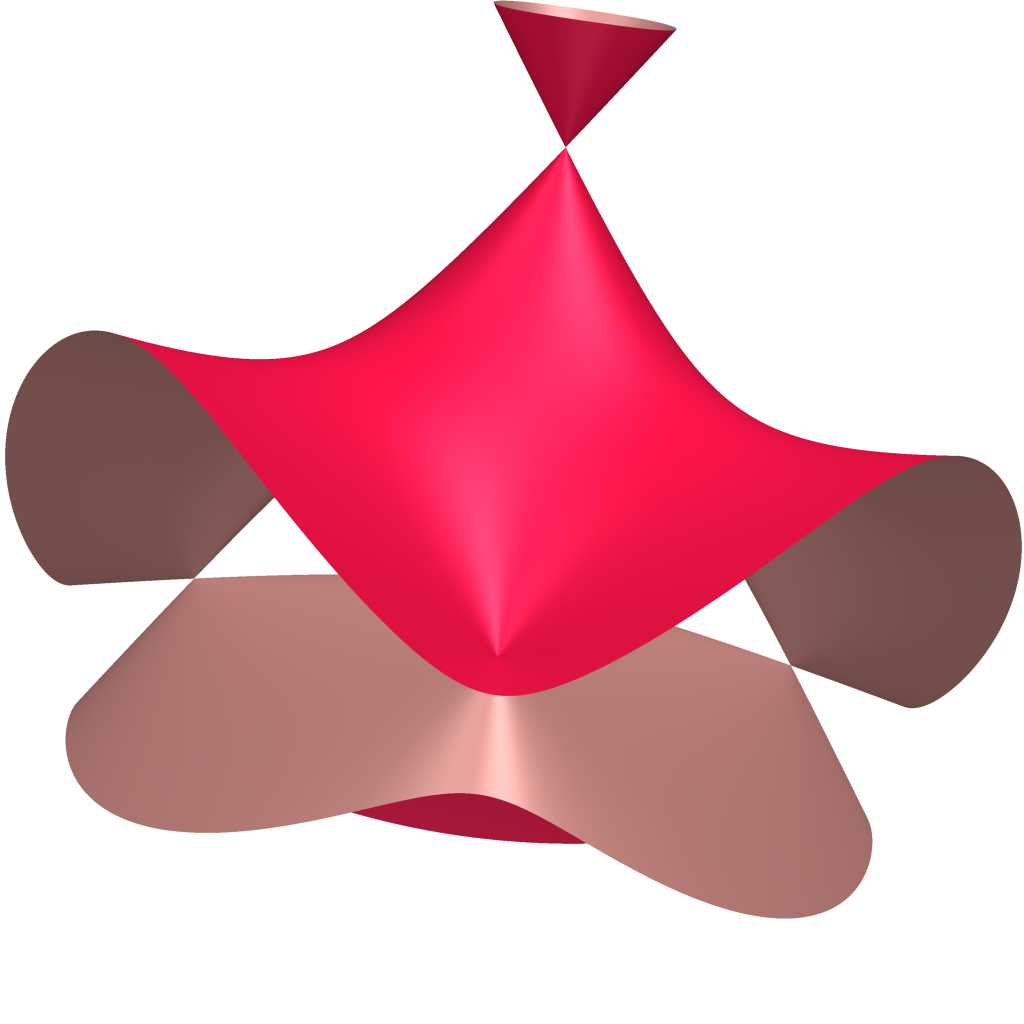
So, also, machen wir mal Grad 3. Grad 3 ist auch aus dem 19. Jahrhundert bekannt.
Es gibt eine Fläche, die sogenannte Cayley Cubic, die durch ein Polynom von
Grad 3 beschrieben ist, die vier Singularitäten hat.
Und die sieht ganz interessant aus, ich beschreibe das jetzt mal so für die
Leute, die sich das vielleicht vorstellen können.
Die sieht eigentlich aus wie so ein Hexenhut oder Zaubererhut,
also so ein geschwungener Hut. Und der Hut hat erstmal eine Spitze.
Die Spitze ist eine Singularität und es ist auch so eine Doppelkegel-Singularität.
Das heißt, da kommt dann wieder bei der Fläche natürlich so ein zweiter Kegel raus.
Und dann hat der Hut, wie die Bodenfläche von einem Tetraeder,
noch drei Punkte, an denen auch so Spitzen entstehen.
Also es ist eigentlich ein dreispitziger Hut. Die Hutkrempe hat drei Spitzen.
Und an diesen drei Spitzen ist noch mal ein Stück der Fläche befestigt,
das sich nach unten öffnet.
Aber insgesamt kommen wir eben auf diese vier Singularitäten,
die Spitze des Huts und die Dreiecken eines Hexenhuts.
Und es sind auch alles solche Doppelkegelsingularitäten, wo sich eben weitere
Stücke in der Fläche anschließen, die dazu führen, dass es so lokal an der Stelle
aussieht wie so ein kleiner Doppelkegel.
Das ist eben das Nullstellengebilde von einem bestimmten Polynom vom Grad 3,
das man auch ziemlich leicht hinschreiben kann. Also für die Fans, ich sag mal den Trick.
Man nimmt die Gleichung 1 durch x plus 1 durch y plus 1 durch z plus 1 durch w.
Also diese vier Brüche aufsummiert. Dann multipliziert man die mit dem Hauptnenner
durch, sodass man auf ein Polynom vom Grad 3 kommt, das keine Brüche mehr enthält.
Also ich multipliziere die einmal mit x mal y mal z mal w durch.
Jetzt habe ich aber noch vier Variablen und dann setze ich noch w als 1 minus x minus y minus z.
Dadurch eliminiere ich das w und dann bekomme ich eine schöne kubische Fläche,
deren Nullstellengebilde diese Kd³ ist.
Ja und um zu zeigen, dass 4 das Maximum ist, ist schon ein bisschen mehr Mathematik
nötig, als man so im Grundstudium lernt.
Da gibt es einige interessante Sätze, auch aus dem 19. Jahrhundert noch.
Es gibt zum Beispiel den Satz, dass jede glatte solche Fläche,
die durch ein kubisches Polynom bestimmt ist, man nennt die auch eine kubische
Fläche, 27 Graden enthält. Okay?
Also, die ist natürlich irgendwie so krumm, diese Fläche, aber wenn sie glatt
ist, keine Singularitäten hat, dann enthält sie 27 Graden.
Es ist erstens erstaunlich, dass sie überhaupt Geraden enthält.
Also irgendwo in dieser krummen Fläche gibt es eine Gerade. Und nicht nur eine,
sondern ein Paar und es müssen immer genau 27 sein.
Und es gibt eine besonders symmetrische Variante davon, die kann man auch 3D drucken.
Also wenn man mal in meinem Büro ist, kann man eine 3D gedruckte Variante von
dieser Fläche sehen, die 27 Geraden enthält.
Man muss dann auch so ein bisschen aufpassen mit den komplexen Zahlen und den
reellen Zahlen, weil viele von den Sätzen, die ich jetzt erwähne,
enthält 27 Grad, gelten eigentlich über den komplexen Zahlen.
Aber es gibt hier auch eben eine reelle Realisierung, wo man die 27 Grad auch
in der reellen 3D-Druckbahnwelt sehen kann.
Aber warum rede ich jetzt über diese 27 Grad?
Also die 27 Grad betreffen ja glatte Flächen.
Und man sollte sich das so vorstellen, dass neben jedem singulären Polynom oder
jeder singulären Fläche liegen auch noch glatte Flächen.
Also der typische Fall ist eine glatte Fläche.
Und wenn ich die Koeffizienten von dem Polynom ein ganz kleines bisschen in
die richtige Richtung verändere, bekomme ich immer eine glatte Fläche.
Man kann das auch sich bei dem Kegel, bei dem Doppelkegel zum Beispiel visualisieren.
Da könnte man einen Parameter einführen, der, wenn ich den ein bisschen in die eine Richtung ändere.
Würde die Fläche zerfallen in zwei flächen die
obere und die untere hälfte und die
kegel werden jetzt nicht mehr spitz sondern abgerundet und
die beiden abgerundeten stellen werden sehr nah aneinander
das wäre dann aber eine glatte fläche und es wäre auch nur eine fläche obwohl
sie jetzt aus zwei hälften besteht wenn ich diesen parameter in die andere richtung
ändere dann würde sich ein loch ausbilden wie ein kleiner schlauch eine kleine
schlauchverbindung zwischen den beiden Kegelhälften und es wäre auch keine Spitze dort mehr.
Also nur durch eine ganz bestimmte Konfiguration von Koeffizienten in dem Polynom
ist es möglich, dass da eine Singularität ist.
Und jetzt ist es so, dass wenn man ein singuläres Polynom, ein kubisches Polynom
hat, was passiert mit den 27 Geraden?
Und das ist Teil dieser Klassifikation oder des Verstehens, wie viele Singularitäten
möglich sind, zu verstehen, was mit diesen Geraden passiert.
Ob die aufeinanderfallen, wie sehen die Konfiguration von den 27 Geraden aus,
wenn man in der Nähe einer Singularität ist und mit in der Nähe meine ich jetzt
Polynome betrachtet, die zwar glatt sind, aber durch eine ganz kleine Veränderung
in ein singuläres Polynom verwandelt werden würden.
Aber wo wir jetzt grad bei 3D-Druck waren, das ist eigentlich auch ein Spannungsfeld.
Also, diese Singularitäten in den Flächen, die stellen natürlich ein Problem dar für 3D-Druck.
Man hat ja da immer so eine Fläche, so einen Punkt, wo das leicht auseinanderbrechen
kann oder im Grenzfall, wenn man beliebig hohe Genauigkeit hat,
überhaupt nicht verbunden hat.
Solche singulären Flächen 3D zu drucken, ist schwierig bis unmöglich.
Also, man muss sich überlegen, was man mit den Singularitäten dann macht oder
wie man die Fläche da zusammenbaut, wenn man die z.B. durch 3D-Druck visualisieren will.
Schon wenn man die auf dem Bildschirm visualisieren will, kommt man in Schwierigkeiten.
Es ist überhaupt eine interessante Fragestellung aus dem Bereich der praktischen
Informatik, wie man so eine Fläche, die als Nullstellenmenge von einem Polynomen
beschrieben wird, wie man die eigentlich darstellt.
Also in so einem 3D-Programm, sodass man die schön drehen kann und so.
Kann man sich so verschiedene Methoden einfallen lassen.
Man könnte zum Beispiel den Raum irgendwie mit so einem Punktegitter überdecken
und immer prüfen, was das Polynom dafür in Wert annimmt.
Und das ist super aufwendig. Und die Bilder, die ich gemacht habe,
die sind mit einem Programm entstanden, das heißt Surfer.
Surfer kommt so ein bisschen wie von Surface. Surface Plotter.
Und das verwendet eine interessante Methode, das schneidet die Fläche mit einer
Geraden, mit einer zufälligen Geraden.
Die zufällige gerade sticht irgendwo durch die
fläche und dann kann man sehr
genau mit dem newton verfahren die punkte
die schnittpunkte von der geraden mit der fläche berechnen und dann hat man
schon mal ein paar punkte ein oder paar von der fläche und das macht man jetzt
immer wieder mit ganz ganz vielen zufälligen geraden.
Und es stellt sich heraus, dass durch die Effizienz des Newton-Verfahrens,
um einzelne Nullstellen zu finden, man damit die Fläche sehr gut plotten kann
und nicht in die numerischen Schwierigkeiten kommt.
Also die beste Methode, um eine gegebenenfalls singuläre Fläche genau zu bestimmen,
sodass man sie plotten kann, ist, sich wieder auf den eindimensionalen Fall
des Findens von Nullstellen von Polynomen in einer Variable zurückzuziehen.
Indem man die Fläche mit einer Geraden schneidet.
Und dann hat man eben die Einschränkung des Polynoms auf die Gerade und dort
wendet man dann die klassischen Nullstellensuchverfahren an.
Ist auch ein gut parallelisierbarer Prozess.
Normalerweise, wenn man so an so einen Funktionsplotter denkt,
würde man ja denken, also wenn man so eine Funktion y gleich f von x,
wie man so eine Schule kennt, ja, fertigen sie eine Skizze des Polynoms an.
Da hat man ja immer diese Paare, also man nimmt ein x und plottet
das f x dazu hat man diese paare x f von
x aber nicht jede von diesen flächen
die wir jetzt hier beschreiben lässt sich überhaupt so schreiben
ja also die diesen plot dem
an der schule gemacht hat da ist das was man
plottet als funktion von einem argument beschrieben
aber hier haben wir eine andere beschreibung als null
stellen menge und nicht jede null stellen menge lässt
sich in so eine wie man sagt parametrische form überführen oder
gegebenenfalls auch nur stückweise und an den singularitäten hat
man dann gegebenenfalls dort auch probleme deswegen
muss man sich eine andere methode einverlassen und dieses surfer ist
ein tolles programm dafür und das schönste an dem programm ist dass man da auch so rumspielen
kann also da könnt ihr euch auch diese rekord flächen alle anschauen und ihr
könnt die farben auch selbst wählen und auch die flächen durch eigene gleichungen
flächen definieren und versuchen damit irgendwas lustiges zu basteln euch mal
so eine fläche zu basteln die aussieht wie eine Teekanne oder so.
Das ist wie so ein kleiner Sport.
Also wenn man so ein paar Tricks kennt, wie man zum Beispiel aus zwei gegebenen
Flächen eine neue konstruiert, die beide Teile enthält.
Das macht man einfach immer, indem man das Produkt von den Gleichungen nimmt,
die die einzelnen Flächen bestimmen.
So kann man dann also wie aus verschiedenen Teilen irgendwas zusammenbauen und
dann kann man sich eine ganze Szenerie als Fläche aufbauen.
An die Rekorde ranzukommen wird damit natürlich schwierig, weil man durch dieses
Produkt neben beim Zusammensetzen den Grad stark erhöht.
Also wir wollten ja uns anschauen, wie viele Singularitäten sind möglich, sortiert nach dem Grad.
Ist vielleicht ein bisschen ein seltsames Spiel, aber in dem Programm seht ihr
als Beispiele einige kuriose Sachen, die so entstanden sind.
Und das Programm gehört zu einer größeren Sammlung mathematischer Exponate,
möchte ich es mal nennen, die heißt Imaginary.
Also ein ganz tolles Open Science Mathematik-Kunst- und Mathematik-Visualisierungsprojekt,
das,
auch.
Schon in verschiedenen...
Museen dieser Welt Exponate ausgestellt hat und ja, wo man sich immer gerne,
Inspirationen für Visualisierung von Mathematik holen kann.
Okay, aber ich will noch mal zurückkommen zu meiner Funktion, die ich hatte.
Also wir hatten, wenn wir im dreidimensionalen sind und Flächenbeschreibung
vom Grad 1 haben wir keine Singularität, Grad 2 ist nur eine Singularität möglich,
Grad 3 sind vier Singularitäten möglich und das ist auch das Maximum Und die
Cayley Cubic realisiert es und jetzt
ist man genau so an der Schnittstelle zwischen Algebra und Geometrie.
Also diese, wie zählt man eigentlich die Singularitäten einer Fläche,
die man jetzt im Sinn hat.
Man kann die natürlich mit Surfer plotten und dann einfach versuchen nachzuzählen,
aber das ist eine krude Methode,
weil man eventuell nicht alle Singularitäten sieht, weil die klein sind,
man muss reinzoomen Und deswegen ist es besser, systematisch vorzugehen und
eben Algebra und Symmetrie-Theorie zu benutzen.
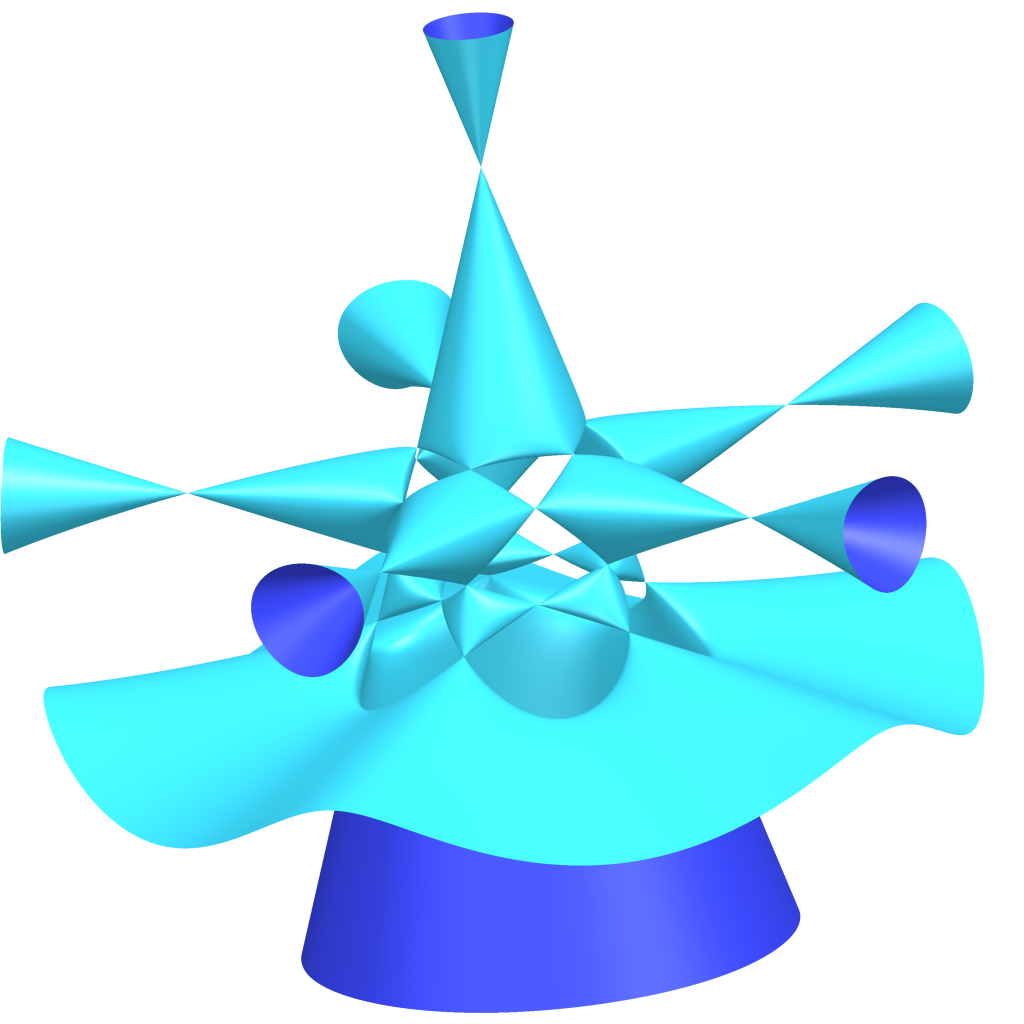
So, jetzt sind wir jetzt 1875, gibt's einen Durchbruch im Grad 4,
da wurde die Kummerquartik gefunden. Es gibt dann immer so lustige Namen für solche Flächen.
Also eine Kubik ist eine Fläche vom Grad 3, eine Quartik ist eine Fläche vom Grad 4.
Und dann darüber werde ich schon so ein bisschen unsicher mit den Worten.
Aber jetzt sind wir noch bei der Quartik.
Die wurde von Ernst Kummer gefunden und heißt deswegen Kummer-Quartik und die
hat 16 Singularitäten und die sieht ungefähr so aus.
Man hat in der Mitte so eine Art Tetraeder.
Und dieser Tetraeder ist aber kein eckiger, kantiger Tetraeder,
wie man ihn kennt, sondern so ein bisschen aufgepustet.
Als ob man da Luft reingepustet hat und dadurch ist der rund geworden, außer an den Spitzen.
Also die Kanten sind weg, ist alles ganz rund, aber die Spitzen sind noch da.
Also der Tetraeder hat vier Spitzen.
Und an jedem von diesen vier Spitzen hängt nochmal so ein kleiner Tetraeder,
der auch aufgepustet ist und nur seine Ecken als Singularitäten über hat.
Und insgesamt kommt man damit auf 4 mal 4 gleich 16 Singularitäten,
alle von diesem Doppelkegel-Typ.
Also in Grad 4 sind 16 Singularitäten möglich und man kann auch zeigen,
dass das die maximale Anzahl ist.
Also diese Zahlenfolge geht weiter, Grad 4, 16.
So, dann 1937 findet Togliatti eine Fläche vom Grad 5, die 31 Singularitäten hat.
Und das ist dann erstmal der Weltrekord für eine Weile.
Und kurioserweise zeigt 1980, also sehr viel später, ein französischer Mathematiker
namens Arnaud Bovy, dass das die maximale Zahl ist.
Und das war schon ein überraschendes Ergebnis, weil man irgendwie mit diesem
1, 4, 16, man hatte irgendwie auf die 32 geschielt, aber tatsächlich ist es nicht möglich.
Die 31 ist das Maximum. Und interessanterweise bei diesem Grad 5 gibt es keine
Verbindung zu Tetraedern oder regelmäßigen Fünfecken oder irgendwie platonischen Körpern.
Also dass da so eine Symmetrie drin steckt, passiert halt manchmal,
aber manchmal auch nicht.
Das Problem ist irgendwie interessanter als gedacht.
Also unsere Folge, die wir fortsetzen wollen, ist jetzt 1, 4, 16, 31.
Also die Zahlologen erwarten, dass die 64 vielleicht jetzt eine obere Schranke in Grad 6 ist.
Aber wenn sie das denken, sind sie auf dem Holzweg.
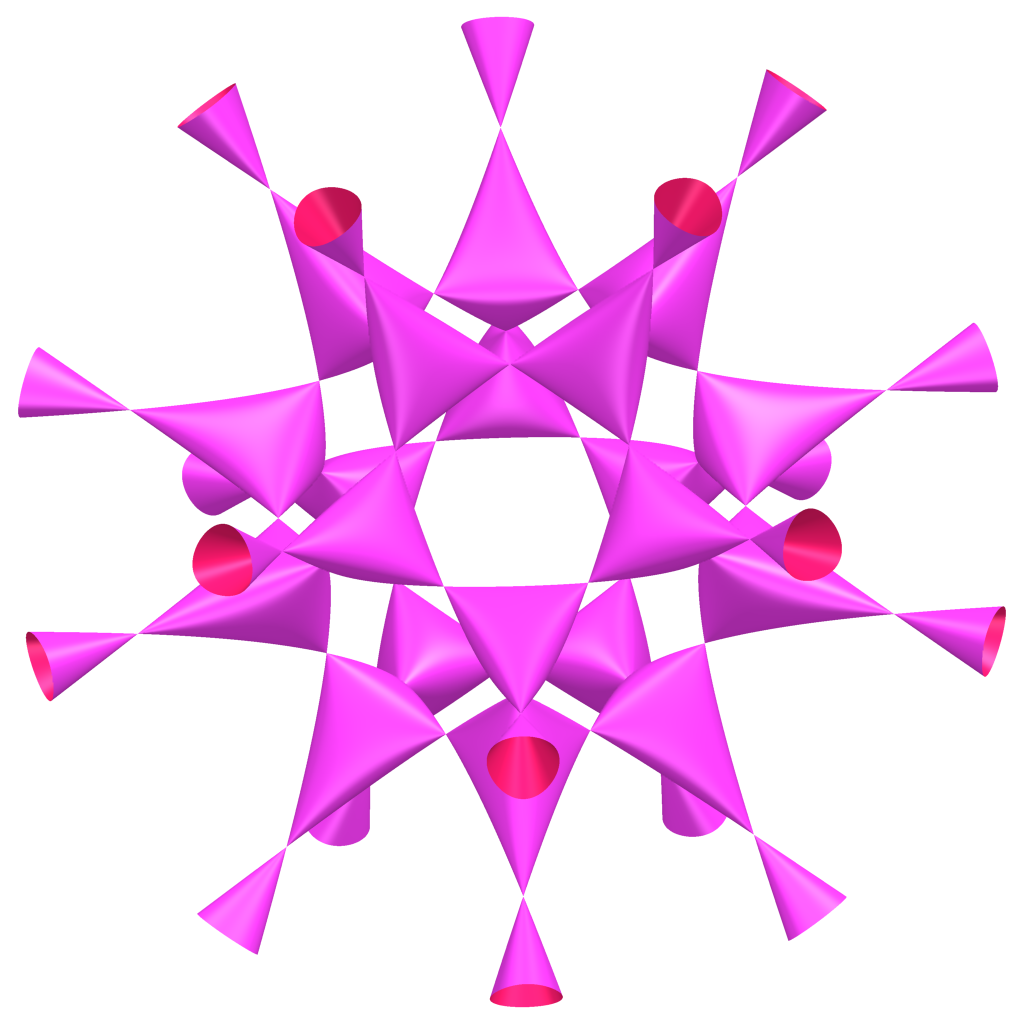
Denn 1996, also schon kurz vor der Jahrtausendwende, fand Wolf Barth,
ein deutscher Mathematiker, die sogenannte Bart-Sextik, die hat 65 Singularitäten.
Also geht noch eins mehr. Also bei der 31 war es eins unter dem erwarteten Wert,
bei der 65 ist es eins über der 64.
Und kurze Zeit später wurde auch gezeigt, dass nicht mehr geht.
Also das war ein überraschendes Ergebnis, da es da auch ein fehlerhaftes Ergebnis
vorher von Severi gab, der angeblich gezeigt hatte, dass 51 das Maximum ist.
Also es gab dann eine Veröffentlichung zu diesem Thema, in der drin stand,
dass 51 das Maximum ist, die sich dann als falsch herausstellte,
nachdem dieses Beispiel gefunden wurde.
Der Beweis, dass 65 aber auch das Maximum ist, wird als richtig angenommen.
Also man hat immer dieses, die Zahl, was ist die maximale Anzahl an Singularitäten,
die möglich ist, wird immer festgelegt, dadurch, dass man ein Beispiel konstruiert,
was viele Singularitäten hat,
zusätzlich noch einen Satz hat, der beschreibt, was das Maximum überhaupt sein kann.
Es ist auch interessant, dass das Maximum überhaupt endlich ist.
Also da muss man natürlich ein paar technische Sachen beachten,
dass man so einen Satz bekommt.
Zum Beispiel spreche ich hier immer über isolierte Singularitäten.
Also man kann auch einfach auf triviale Art und Weise, indem man zum Beispiel
ein Polynom quadriert, eine Fläche konstruieren, die überall singulär ist,
nach einer formalen Definition von Singularität, die ich ja gar nicht gegeben habe.
Aber solche Fälle will man mal auslassen und dann gibt es schon den älteren
Satz, der zumindest sagt, dass die Anzahl der isolierten Singularitäten immer endlich ist.
Und formal gibt es dann auch so verschiedene Typen, Klassifikationen von Singularitäten,
wie es in der Mathematik immer so ist.
Gibt es eine ganze Singularitäten-Theorie, die verschiedene Singularitäten unterscheidet.
Aber das ist für unsere kleine Zahlenfolge hier heute nicht so wichtig.
Interessanterweise hat die Sextik, die Bart gefunden hat, wieder eine Symmetrie,
die zu einem platonischen Körper gehört, nämlich eine Ikusaeder-Symmetrie.
Also ihr seht die jetzt wahrscheinlich auch gerade auf eurem Podcast-Player,
und wenn man jetzt den Ikusaeder da irgendwie reinlegen würde und dann Spiegelt
oder so oder Symmetrieoperationen des Ikusaeders anwendet, wird die auch wieder
auf sich selbst abgebildet.
So nun sind wir bei D gleich 7 angekommen und D gleich 7 ist sozusagen der Stand der Forschung.
Es gibt eine Fläche von Oliver Laabs, die hat 99 Singularitäten und wir sind
jetzt weg von den zwei Potenzen.
Es gibt auch einen Satz, dass die maximale Anzahl 104 ist und dazwischen ist noch alles möglich.
Also 99 könnte das Maximum sein, 100, 101, 102, 103 oder 104.
Also Ihr könntet jetzt quasi hingehen mit Surfer und dort Flächen von Grad 7
erzeugen und schauen, ob ihr vielleicht 100 Singularitäten erzeugen könnt.
Aber es ist nicht so einfach. Also wenn ihr da eine neue Methode findet,
um so super singuläre Flächen zu erzeugen, dann könnte man das ja wahrscheinlich
schon als Promotion irgendwo einreichen, wenn es nicht nur das Beispiel ist.
Der Oliver Lobster hat das auch richtig gefeiert, seine Entdeckung,
und hat dann sogar so einen kleinen Shop aufgemacht, wo man diese Flächen dann auch kaufen kann.
Es ist ja so, dass die 3D-Druckvariante nicht so erfolgreich ist.
Und deswegen, wenn man so eine Fläche visualisieren will, auf elegante Art und
Weise, kann man die in Glas einlasern.
Ich weiß gar nicht, wie ich das jetzt beschreiben soll, da gibt es auch einen Mausfilm darüber,
wie das gemacht wird, dass man hat so einen Glaswürfel, der ist ja eigentlich
durchsichtig, aber in dem werden einzelne Punkte mit Lasern so verändert,
dass die dann nicht mehr durchsichtig sind und daraus entsteht dann eben diese,
Visualisierung der Fläche.
Kann ich auch mal verlinken, bekomme ich natürlich aber jetzt nichts für diese
kleine Werbung, das nur als Full Disclosure.
Für D gleich 8 liegt die Zahl zwischen 168, wofür eine Fläche bekannt ist,
und 174, was die bisher beste obere Schranke ist.
Für allgemeines D hingegen ist fast nichts explizites bekannt,
außer dass die Anzahl der Singularitäten kubisch im Grad ist.
Und sie liegt zwischen 5 zwölftel d hoch 3, wenn d der Grad ist, und 4 neuntel d hoch 3.
Ein Ergebnis von Sonja Breske, Oliver Labs und Duco von Straten von ungefähr 2005.
So und das war auch schon die Geschichte dieser kuriosen Zahlenfolge.
Ich sage sie euch noch mal. Also die Zahlenfolge lautet 1, 4, 16, 31,
das war für grad 5 und für grad 6 die 65.
Und grad 7 irgendwas zwischen 99 und 104.
Für grad 8 irgendwas zwischen 168 und 174. Und niemand weiß so richtig,
wie die Folge weitergeht.
Und ja, wir sind gespannt auf die weiteren Entwicklungen in diesem Jahrhundert und Jahrtausend.
Und ich wünsche euch eine gute Zeit und viel Spaß mit den singulären Flächen,
falls ihr damit rumspielen solltet. Ciao!

