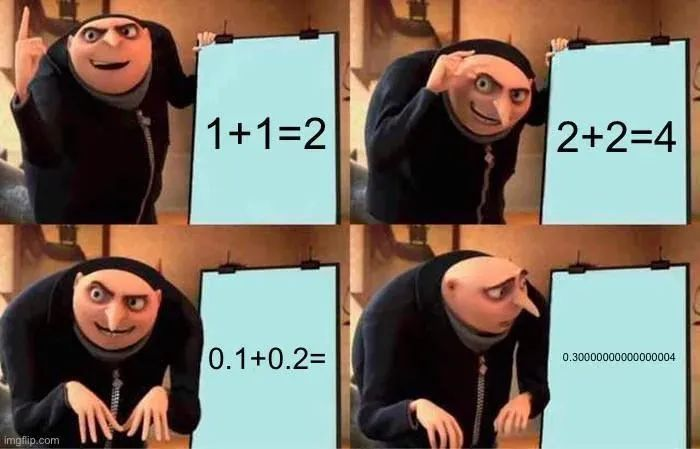Mathias Magdowski ist wieder da und wir sprechen erstmal über diese zwei Bilder:
Offensichtlich läuft da irgendwas schief mit den Zahlen, aber vielleicht ist das auch alles gar nicht falsch, sondern entspricht genau den gültigen ingenieurwissenschaftlichen Standards für Zahlen?
- Unsichtbar wird der Fehler, wenn sich alle dran gewöhnt haben (Wolfgang Coy)
- Der Dezimalpunkt ist 150 Jahre älter als gedacht (Nature)
- Auslösung in der numerischen Mathematik
- IEEE Standard 754
- Gleitkommaarithmetik auf dem Prüfstand (Siegfried Michael Rump)
- Implementierung der Grundrechenarten
- GNU MPFR Library
- Einfluss verschiedener Datenformate auf frequenzabhängige mit Impedanzanalysatoren gemessene Impedanzen (Mathias Magdowski und Matthias Hampe)
- Hidden Figures: When did John Glenn ask for ‚the girl‘ to check the numbers?
- Ariane 5 Crash beim Erstflug
- Mathias‘ iterative Octave-Rechnung zum Ausprobieren
Feedback gerne auf Mastodon @Eigenraum@podcasts.social, an feedback (bei) eigenpod.de oder in die Kommentarspalte auf der Episodenseite.
Verwandte Folge:
Automatisch generiertes Transkript (nicht geprüft)
Thomas Kahle
6, 3, 6, 0, 7, 6, 0, 8,
Hallo zusammen und willkommen bei einer neuen Folge Eigenraum.
Ich bin heute mal nicht in meinem sonstigen Podcast-Umgebung,
in meiner Location, sondern in der Fakultät für Elektro- und Informationstechnik.
Und ich bin auch nicht alleine hier, sondern Matthias ist wieder da.
Matthias war ja schon in Folge 22 dabei, als wir über Einheiten geredet haben.
Willkommen zurück, Matthias. Hallo.
Mathias Magdowski
Hallo, hallo. Ja, wir sitzen auch wieder genau in dem gleichen Raum,
in dem wir die Eigenraum 22 Folge aufgenommen haben.
Ein kleiner, schnuckliger Besprechungsraum bei uns in der Fakultät.
Thomas Kahle
Ja, und wir wollen mal wieder etwas plaudern, ohne aber jetzt das Konzept Laber-Podcast
vielleicht auszureizen. Natürlich thematisch fokussiert. Und das Thema kam zu
mir von dir über ein lustiges Bildchen, was ich mal bekommen habe.
Und auf dem Bildchen, ich beschreibe das jetzt erstmal so ein bisschen,
sehe ich ein Werbeplakat von einer Firma, einem Laden vielleicht,
dem Wahnsinnsschnellverkauf WSV, der verkauft Restposten und Einzelstücke bis
zu 70 Prozent reduziert und verkauft hier ein Pasta Maker.
Was ist eigentlich Pasta Maker? Also ein Elektrogerät, was Nudeln herstellt?
Mathias Magdowski
Eine Nudelmaschine, die elektrisch betrieben ist? Ich würde ja vermuten irgendwas,
was Nudeln kocht, so ähnlich wie ein Reiskocher, wobei es mir dafür eigentlich
relativ teuer vorkommt.
Thomas Kahle
Genau, der Originalverkaufspreis. Trotz der 70% Rabatt. Es sind ja gar keine,
also wer Social Media Kanäle vom Eigenraum abonniert, hat es vielleicht schon gesehen, dieses Bild.
Also es ist dort verewigt und der Originalverkaufspreis
war 297,99,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00,00 55,99,8
Euro reduziert und kostet jetzt nur noch 223,99,2 Euro.
Und das ist unser Thema. Warum ist das unser Thema? Wir wollen heute nämlich mal über Zahlen reden.
Mathias Magdowski
Ja, und ich glaube, du hast ja schon häufiger mal über Zahlen geredet,
aber die Idee ist mal ein bisschen über die Hintergründe dieser Rechnung da
oder also was da potenziell vielleicht schiefgelaufen ist bei der Erstellung dieses Plakates,
nämlich so wie Computer mit Zahlen rechnen.
Und das Zauberwort oder das Fachwort dafür heißt Gleitkomma-Arithmetik und ich
bin ja eher in den Ingenieurwissenschaften unterwegs als in der Mathematik und
da beschäftigt mich das doch hier und da mal,
immer nämlich dann, wenn man irgendwas mit dem Computer rechnet oder vielleicht
auch mal mit dem Taschenrechner rechnet oder so numerische Simulationsprogramme
bemüht, um irgendwelche Netzwerke auszurechnen oder Felder zu berechnen,
dann sind natürlich alle Ergebnisse und alle Zwischenergebnisse und Endergebnisse
und alle Parameter, die man irgendwie reintut und mit dem man den Computer füttert,
sind immer solche Zahlen und da passieren dann eben wundersame Dinge manchmal,
also so wie jetzt hier auf diesem, recht offensichtlich auf diesem Werbeplakat.
Und das habe ich jetzt vorher nicht gepostet. Noch ein weiteres kleines Meme-Teil,
das kann ich auch kurz beschreiben.
Also das ist so dieses typische Gru-Meme mit der Person aus dem Minions-Film
und dann mit diesen vier Kacheln, die man so kennt.
Und in der ersten steht 1 plus 1 ist 2. Okay, da würden wir alle zustimmen, das ist so in Ordnung.
Und im nächsten steht, glaube ich, 2 plus 2 sind 4. Okay, ja,
das passt auch so nach den Grundgesetzen der Mathematik.
Und dann steht im nächsten 0,1 plus 0,2 und das Ergebnis im dritten ist dann
eben auch nicht 0,3, sondern 0,3, 0,0, 0,0, 0,0, auch etliche Nullen und dann
hinten auch irgendwie eine 1 oder eine 2 oder irgendwie sowas.
Und tja, solche Sachen kommen auch tatsächlich in meinem täglichen Leben als
Ingenieur immer mal irgendwie vor und so das Standardbeispiel,
was ich dann immer ganz gerne zeige, um das Studierenden zu demonstrieren oder
sie irgendwie für diese Problematik zu sensibilisieren,
über die sich sonst glaube ich überhaupt niemand Gedanken macht,
weil alle immer davon ausgehen, ja Computer wird schon irgendwie richtig rechnen.
Es gibt auch ein schönes Buch oder Skript oder Kapitel, was wir mal verlinken
können, von Wolfgang Coy, glaube ich, auch Professor in Berlin,
wenn ich es richtig im Kopf habe.
Das heißt den schönen Titel Unsichtbar wird der Fehler, wenn sich alle daran gewöhnt haben.
Und das Beispiel, was ich immer zeige und demonstriere, das kann man in Octave
oder in MATLAB irgendwie sehr schön und einfach immer zeigen,
ist, also du rechnest 1 minus 1, ist klar, ist 0.
Und rechnest zum Beispiel 10 hoch minus 16 dazu.
Dann rechnet der Computer aus 1 minus 1 plus 10 hoch minus 16 ist 10 hoch minus
16, 1 e minus 16 geschrieben. So kommt das ja dann in MATLAB raus.
Jetzt haben wir ja alle mal so irgendwie in der Schule gelernt,
für die Addition gilt ein Kommutativgesetz.
Man kann die Reihenfolge der Summanden vertauschen. Und wenn man jetzt die gleiche
Rechnung einfach ein bisschen anders es in einen Oktav reinschreibt und rechnet 1 plus 10 hoch minus 16.
Und dann erst die Minus 1, dann kommt, obwohl das ja jetzt erstmal genau exakt
prinzipiell die gleiche Rechnung ist, kommt eben nicht 10 hoch minus 16 raus,
sondern es kommt einfach 0 raus.
Weil die 10 hoch minus 16 einfach praktisch wie verschluckt wird,
wenn man die auf die 1 drauf addiert.
Und das ist, glaube ich, für viele immer irgendwie so ein Aha-Effekt,
dann mal darüber nachzudenken, Moment, wie macht das so ein Computer jetzt eigentlich im Hintergrund?
Wie rechnet Octave das meinetwegen oder Python oder eben meinetwegen auch so
ein kommerzielles Programm wie MATLAB?
Und ich meine, da können wir jetzt versuchen, uns ein bisschen drüber zu unterhalten
und mal so das, was wir jeweils vielleicht so wissen, versuchen in den Ring
zu werfen, ohne jetzt alle in die tiefsten Abgründe der Gleitkomma Arithmetik,
so heißt ja das Zauberwort dafür, irgendwie abzutauchen.
Aber das ist für mich immer so ein spannender Aufhänger, über diese Problematik nachzudenken.
Thomas Kahle
Ich meine, die erste Frage ist ja vielleicht, was überhaupt wir beschreiben
wollen. Ich denke mal, wir wollen reelle Zahlen beschreiben.
Oder würdest du da jetzt von abweichen?
Mathias Magdowski
Ich würde sagen, ja. Ich meine, in der Elektrotechnik brauchen wir ab und zu
auch mal komplexe Zahlen.
Thomas Kahle
Okay, eine komplexe Zahl sind zwei reelle Zahlen.
Mathias Magdowski
Sind zwei reelle Zahlen.
Thomas Kahle
Ja, okay. Und ...
Da haben wir ja erstmal so ein grundlegendes Problem, dass in so einer reellen
Zahl unendlich viel Information drinstecken kann.
Mathias Magdowski
Genau, die kann beliebig lang werden.
Thomas Kahle
Und die meisten reellen Zahlen, und das kann man wirklich präzise machen,
sind ja auch ziemlich schlimm.
Also die meisten reellen Zahlen sind sogar so, ich weiß nicht,
ob ich da schon mal eine Folge drüber gemacht habe, die sind so nicht.
Doch, die Folge unreale Zahlen enthält mehr darüber, die verlinke ich dann auch nochmal.
Die meisten reellen Zahlen sind nämlich sogar so nicht berechenbare Zahlen.
Die sind von der Natur, dass man nicht mal ein Computerprogramm angeben kann,
was alle ihre Stellen ausrechnet.
Also Pi enthält zwar unendlich viel Information, wenn man diese ganzen Dezimalstellen
hat, aber man kann natürlich einen Algorithmus angeben, der immer mehr Stellen
produziert, aber für die meisten reellen Zahlen ist es quasi noch schlimmer.
Also gehen wir irgendwie davon aus, dass die Zahlen, die wir im Computer irgendwie
abspeichern und die wir berechnen können, dass es davon immer noch genug gibt,
dass wir alle Sachen, die wir in Octave ausrechnen wollen, auch ausrechnen können.
Da habe ich übrigens neulich jetzt gerade den Dezimalpunkt, wusstest du,
wann der Dezimalpunkt zum ersten Mal aufgetaucht ist?
Mathias Magdowski
Oh nee.
Thomas Kahle
Da gab es jetzt gerade so einen Nachrichtenbeitrag in Nature,
dass der nämlich jetzt gerade 150 Jahre jünger geworden ist.
In den 1440er Jahren gab es so astronomische Berechnungen, wo zum ersten Mal
diese Idee des Dezimalpunkts zum Abtrennen der Bruchteile von Zehen auftaucht.
Und vorher war es irgendwie erst um 1600 der Fall.
Mathias Magdowski
Also er ist jetzt eigentlich älter geworden. Der ist älter geworden, genau.
Thomas Kahle
Man hat eine ältere Quelle, wo diese Notation auftaucht.
Mathias Magdowski
Ja gut, und die Frage ist natürlich, ob man nicht vielleicht die Idee noch älter
ist, dass einfach nur dann keiner aufgeschrieben hat oder die Quelle einfach
nicht mehr verfügbar ist.
Thomas Kahle
Ja, da ist man jetzt schon auf so sehr alte Dokumente.
Mathias Magdowski
Genau, nichts, was im Altertum dann schon bekannt war und auf irgendwelchen Steintafeln oder …,
Die sich ja länger halten als gedruckte Werke.
Thomas Kahle
Aber ich denke mal, so Anfang 20. Jahrhundert kann man irgendwie in die Verlegenheit,
algorithmisch zu arbeiten mit Zahlen, mit reellen Zahlen, vielleicht auch mit
Approximationen von Zahlen.
Ich meine, letztendlich, wenn wir die Physik beschreiben wollen oder die Welt
um uns herum, werden wir irgendwie immer mit Messfehlern konfrontiert sein.
Das heißt, Approximationen reichen uns, oder?
Mathias Magdowski
Genau, und ich, also zumindest so, wie ich jetzt das verstanden habe,
gab es früher als Computer jetzt nicht super leistungsfähig waren und nicht
sehr viel Speicher hatten und man eben auch mit sehr geringer Unsicherheit ja
dort brechend Zahlen auskommen musste.
Gab es auch Leute, die eher dann
noch ihrem analogen Messschieber vertraut haben, weil der eben mit einer,
analogen und nicht gequantelten, nicht diskretisierten Darstellungsweise der
Zahlen dann ja vielleicht einem eine bessere Genauigkeit Vorgaukelt,
ob die dann tatsächlich so viel besser ist, wenn man da mit dem Messschieber
oder sozusagen mit dem Rechenschieber irgendwas abliest, der mal hingestellt.
Aber klar, es ist natürlich eine Herausforderung, irgendwie so einen großen
Zahlenbereich, also sehr kleine Zahlen, sehr große Zahlen jetzt in einen begrenzten
Speicher reinzupacken.
Thomas Kahle
Also meine erste naive Idee, und ich glaube, das ist die Fixpunkt-Methode,
nee, nicht Fixpunkt-Methode, die Fixkomma-Arithmetik, ist, ich nehme einfach
mal eine ganze Menge Bits, sagen wir 100,
und dann speichere ich einfach 100 Nachkommastellen in den 100 Bits ab.
Das Problem ist, ich kann dann sehr genau diese Zahlen zwischen 0 und 1,
nee, zwischen 1 und 2, da kommt drauf an, was ich mir vor dem Komma vorstelle, abspeichern, oder?
Mathias Magdowski
Ja, also ich meine, bleiben wir
vielleicht mal bei natürlichen Zahlen oder bleiben wir bei ganzen Zahlen.
Ich meine, dann kann ich ja mit so und so viel Bit irgendwie einen begrenzten
Zahlenraum darstellen.
Ja, und also mit 8 Bit meinetwegen 256 verschiedene Zahlen. Das kann man sich
irgendwie ganz gut vorstellen.
Und jetzt könnte man natürlich sagen, jetzt mache ich so eine Festkomma- Arithmetik
und mache, anstatt dass ich die Zahlen von,
1 bis 256 oder von 0 bis 255 darstellen kann, mache ich einfach von 0 bis 2,55 zum Beispiel.
Dann könnte ich eben mit festen Cent, wenn man jetzt mit Geld rechnet,
alles von 0 bis 2,55 Euro irgendwie darstellen und rechnen und hätte genau diese
Genauigkeit immer auf einen Cent bezeichnet.
Das klingt jetzt erstmal eigentlich wie eine gar nicht wahnsinnig schlechte
Idee und wenn man mit Geld rechnen will, ist das zum Beispiel auch ganz gut bestimmt,
aber wenn man jetzt so in der allgemeinen Mathematik oder Ingenieurwissenschaft
oder Physik unterwegs ist, dann hat man eher so das Problem,
ich will sehr absolut kleine Unterschiede zwischen kleinen Zahlen immer noch
genauso gut darstellen,
wie Unterschiede zwischen großen Zahlen relativ gesehen.
Also wenn man jetzt bei diesem Beispiel bleibt mit den 2,55 Euro,
dann sind das ja immer feste Stufen.
Ich kann immer Unterschiede von einem Cent darstellen.
Aber das will ich ja gar nicht. Ich will ja eigentlich so relative Änderungen
von Zahlen darstellen, damit ich so dieses ganz kleine und ganz große,
weil ich meine, wenn ich jetzt irgendwie ein paar Millionen habe,
wenn man das mit dem Geld jetzt mal weiterspinnt, ist mir das doch egal.
Bei ein paar Millionen sind die Cents auch egal.
Thomas Kahle
Das ist auch so eine Universalitätsfrage. Der Computer soll eben nicht nur an
ein Problem angepasste Rechenoperationen unterstützen,
sondern im gewissen Sinne die universelle Maschine sein, die eben diese großen
Beträge dann auch abbilden kann, sich an die Problemsituation anpassen kann. Genau.
Mathias Magdowski
Und für Finanzmathematik ist das bestimmt eine total schlaue Idee,
das mit so einer Festkomma-Arithmetik zu machen.
Aber für alle anderen Probleme, also wenn man jetzt an die Physik denkt,
wenn man an ingenieurwissenschaftliche Probleme denkt, dann ist mir das bei
ein paar Millionen ist da egal, ob da noch 0,0 irgendwie dazukommen oder nicht.
Aber dann möchte ich eben, wenn ich ganz kleine Zahlen habe,
irgendwas im Nanometer-Bereich, dann möchte ich da trotzdem noch ganz kleine
Unterschiede. Also braucht man irgendwas, was eine vergleichbare Genauigkeit bietet.
Erstmal unabhängig davon, wie groß die Zahl absolut gesehen ist.
Thomas Kahle
Ja, und das ist diese Gleitkomma-Arithmetik. Und die Idee ist doch eigentlich ganz einfach.
Ich nehme einfach die Information, wo ist eigentlich das Komma,
und speichere die auch noch mit ab.
Mathias Magdowski
Genau.
Thomas Kahle
Also ich habe eine Zahl, die kann ich mir jetzt als ganze Zahl vorstellen.
Und sagen wir mal die 255, die du eben gerade schon hattest.
Und die kann jetzt zählen als 255.
Als 2.550, als 25.500 oder in die andere Richtung eben auch als 25,5 oder 2,55
oder 0,255, wenn ich noch Informationen darüber speichern kann,
wo relativ zum, sagen wir, der Anfang der Zahl das Komma ist.
Und das ist doch eigentlich schon die Idee von der ….
Mathias Magdowski
Das ist letztendlich die ganze Idee von Gleitkommazahlen und das,
was dann davor steht, also jetzt in unserem Fall die 255,
das nennt man Mantisse üblicherweise und dann gibt es eben noch hinten eine Potenz und die,
dann muss man eben ein paar oder eine gewisse Anzahl von Bits in seiner Zahl
reservieren für diese Mantisse und die restliche Anzahl von Bits eben für diesen Exponenten.
Und ja, vielleicht braucht man noch ein Bit für das Vorzeichen oder vielleicht
baut man das Vorzeichen irgendwie anders in die Zahl rein und dann gibt es noch
einige Herausforderungen bei der Rechnung, die können wir gleich noch versuchen
irgendwie ein bisschen zu erklären und zu besprechen und dann ist vielleicht noch die Frage,
irgendwie brauche ich auch eine Null, wie gehe ich damit um?
Thomas Kahle
Ist eigentlich die Addition und Multiplikation, was man so mit Zahlen machen
will, ist die trivial in dieser Darstellung?
Ja, also wenn ich mir das jetzt als Produkt vorstelle, Ich habe diese Mantisse oder mal.
Mathias Magdowski
Also ich glaube, die Multiplikation ist noch am trivialsten,
weil ich meine, ich multipliziere die Mantissen miteinander.
Thomas Kahle
Und addiere die Exponenten.
Mathias Magdowski
Und addiere die Exponenten, ganz genau. Und bei der Addition ist es tatsächlich,
glaube ich, ein bisschen schwieriger, weil damit man die Addition vernünftig
machen kann, muss man die Zahlen beide auf den gleichen Exponenten erst mal bringen.
Thomas Kahle
Und damit sind wir wieder bei deiner 1 plus 10 hoch 16, stimmt's?
Mathias Magdowski
Genau.
Thomas Kahle
Also ist Folgendes passiert, die Information, die 1, die vorm Komma steht und
die 10 hoch minus 16 waren es ja, das ist noch eine 1, die aber so weit entfernt
ist davon, dass da in diesem Datenformat, das da benutzt wurde, nicht genug ist.
Der Exponent ist übergelaufen.
Mathias Magdowski
Ich würde vermuten, dass die Mantisse nicht ausreichte. Die wurde dann einfach zu null gerundet.
Also der größere Exponent gewinnt dann in dem Fall.
Und bei der 10 hoch minus 16 muss man dann diese verbleibende 1 so weit nach
hinten schieben, dass die dann, dass da nicht genug Stellen in der Matrice sind,
sodass die dann wegfällt.
Und diesen, also ja, da gibt es ziemlich viele verschiedene Ideen und Formate,
wie man so Gleitkommazahlen speichern kann, die sich irgendwie auch aus der
Historie entwickelt haben.
Seit den 1980er Jahren ist ein IEEE-Standard, dessen Zahl ich jetzt nicht im
Kopf habe, den können wir verlinken, der tut, glaube ich, auch nichts der Sache.
Aber man spricht dann von IEEE-Gleitkommazahlen.
IEEE ist was, was aus der Elektrotechnik kommt, Institute of Electric Electronic
Engineers, die aber natürlich auch irgendwie eine
größere Community von ComputerwissenschaftlerInnen in sich vereinigen.
Thomas Kahle
Ja, da muss man immer nach Jahr gucken. Also ich glaube, welche Teile von Mathematik
Teil von Wirtschaftswissenschaften, Operations Research, Electrical Engineering,
Informatik waren, das hat sich dann auch immer je nach Jahrzehnt,
in dem man schaut, dann geändert.
Mathias Magdowski
Und Intel, die ja demnächst vielleicht nach Magdeburg kommen,
die stecken da auch irgendwie mit drin, also weil da ging es um einen Gleitkommaprozessor
von denen, wo man eben mal gesagt hat, lass es uns mal einmal,
wie das so mit so Standardisierung ist,
lass es uns mal einmal irgendwie vernünftig aufschreiben, wie wir irgendwie
damit umgehen wollen, dass das für alle danach ungefähr ähnlich ist und man
eben nicht so wie vorher vielleicht das Problem hatte, wenn man verschiedene
Rechnungen auf verschiedenen Computern macht, kommen verschiedene Ergebnisse dabei raus.
Und ja, zumindest in diesem I3B-Standard steckt dann die genaue Vorgehensweise eben drin.
Thomas Kahle
Eine interessante Sache ist, dass die Zahlen dann nicht mehr gleich verteilt
sind, die man abspeichern kann.
Also grundlegendes Problem ist, man kann nur diskrete Menge von Zahlen,
die übrigens alle rational sind, also wir wollten mal über reelle Zahlen sprechen,
aber natürlich speichern wir nur rationale Zahlen immer ab.
Und diese diskrete Menge der rationalen Zahlen, die ist jetzt überhaupt gar
nicht gleich verteilt über die Zahlen, sondern die wird halt eben nach außen hin immer gröber.
Das kann man sich ja auch zum Beispiel vorstellen, also wenn der Exponent,
wenn man so eine große Zahl abspeichern
will, dass man dann gar keine Nachkommastellen mehr zur Verfügung hat.
Und das ist ja auch genau das, was wir vorhin als Ziel ausgegeben haben.
Wenn wir über Millionen und Milliarden reden, dann machen die einzelnen Cent
keinen Unterschied mehr.
So werden die Zahlen zur Null hin immer dichter.
Mathias Magdowski
Genau, also weil man dann ja den Exponenten eben immer kleiner oder negativer
machen kann und dann werden die Zahlen,
wird die Stufung da immer feiner, aber das ist ja genau das vorher Besprochene,
das man eben haben möchte, dass da die Genauigkeit dann zunimmt und nach außen
nimmt die Genauigkeit ab.
Und ich meine das, um jetzt nochmal kurz auf das Problem mit dieser Addition
zurückzukommen, also das, was man mit der Mantisse dann üblicherweise macht,
die wird eben normiert oder normalisiert, da gibt es so verschiedene Begrifflichkeiten,
also entweder dieses Normalisieren heißt, man bringt die, zum Beispiel wenn
man jetzt im Dezimalsystem bleibt,
wäre die zwischen 1 und 10 und danach,
wenn ich eben über die 10 gehe,
würde ich anstatt dessen den Exponenten eben um 1 erhöhen.
Und dieses Normieren heißt eben, ich bringe das zwischen 0,1 und 1 jetzt im Dezimalsystem.
Oder wenn man jetzt binär, Computer speichern, das ist ja typischerweise binär,
dann wäre das Normalisieren eben zwischen 1 und 2, das Normieren zwischen 1,5 und 1.
Und also bei der Addition, wenn man jetzt diese Zahlen, zwei unterschiedliche
Zahlen addieren möchte, dann liegen die ja erstmal in dieser entweder normierten
oder normalisierten Form vor.
Jetzt, wenn die unterschiedliche Exponenten haben, muss man die erstmal denormalisieren,
auf einen gemeinsamen Exponenten bringen, dann wird eben die Mantisse größer, kleiner.
Dann gibt es eventuell diesen, dass durch Rundungsfehler Zahlen verschluckt
werden und am Ende wird man das Ergebnis wieder normieren oder normalisieren,
um das wieder so in den normalen Bereich reinzubringen.
Und genau dieses, durch dieses Denormalisieren, Runden, Normieren,
ja, kommt dann der am Anfang besprochene Fehler mit die 10 hoch minus 16 wird
zum Beispiel irgendwie verschluckt.
Thomas Kahle
Ja, und sag mal, es gibt jetzt diesen IEEE-Standard, der betrifft aber jetzt so fixe Längen?
Oder gibt es wahrscheinlich noch mehr Standards? Also es gibt ja auch,
worauf ich gerade hinaus will, es gibt ja auch diese C-Bibliothek MPFA,
die beliebige Präzision zulässt oder zumindest irgendwie Standards dafür implementiert.
Also wenn ich mir jetzt sage, okay, ich will ja jetzt einen Algorithmus schreiben.
Mathias Magdowski
Der an der Stelle … Der zum Beispiel hier auf unendlich viele oder auf ziemlich
viele Nachkommastellen berechnet.
Thomas Kahle
Genau, also dann könnte ich mir natürlich meine eigene Datenstruktur schreiben,
die einfach diese Nachkommastellen da irgendwie abbildet, aber vielleicht kann
ich auch irgendwie standardisieren,
eine beliebige Präzision, reelle Zahlabbildung, das könnte ich dann einfach, indem ich die,
also ich meine, wie macht man es bei großen ganzen Zahlen, ja?
Diese Implementierung, die nimmt sich dann immer, wenn mehr Platz benötigt wird,
nimmt sie sich halt noch eine Zweierpotenz dazu,
indem sie irgendwie noch so ein Byte oder so extra reserviert und dann braucht
man eben da diese Speicherverwaltung und die ganzen adaptiven Algorithmen eben,
die bei der Addition dann aufpassen.
Also wahrscheinlich könnte man das auch machen, indem man einfach,
letztendlich hat man es wieder zurückgeführt, auf einfach größere Ganzzahlen
abzuspeichern und größere Exponenten muss man gegebenenfalls auch noch abspeichern.
Also man hat die beiden Datenstrukturen, die Mantisse und den Exponenten und
wenn man die jetzt als beliebige Größe Integers implementiert,
dann ist man doch eigentlich schon fast fertig, oder?
Mathias Magdowski
Wahrscheinlich ist das so, ja. Also da steckt ja auch nicht,
ich habe selten in meinem Leben Computer sehr hardwarenah programmiert,
um jetzt an diese Herausforderung reinzukommen.
Aber klassischerweise, ich meine, alle Programme, mit denen man so im normalen
Leben umgeht, speichern das immer als so ein 32-Bit-Float.
Und im Normalfall hat man damit ja irgendwie eine Genauigkeit,
die schon ziemlich gut ist.
Also ich glaube, viele Probleme, von denen man so in der Literatur liest,
Die treten eben dann auf, wenn man nur mit einem 16-Bit-Mikrocontroller meinetwegen
dann irgendwie was rechnet, dass dann da auch meinetwegen mal sowas aufkommt.
Ich nehme eine Zahl, quadriere die und rechne die Wurzel wieder aus der Zahl
und dann kommt eben nicht mehr genau das Gleiche raus.
Also was, glaube ich, in diesem I-Trip-E-Standard so drin steckt.
Dass gefordert wird, dass das Ergebnis immer mindestens so genau ist wie sowieso
die Rundung, die man eben macht.
Also dass das Ergebnis einer Rechnung der Fehler nicht größer ist als den Fehler,
den man sowieso durch die Rundung machen würde.
Thomas Kahle
Könnte es nicht sein, dass man dann dafür für die Eingabe mehr Genauigkeit braucht?
Doch, so ist es doch. Also wenn ich zwei Zahlen addiere, dann nehme ich diese eins.
Also dein Anfangsproblem ist doch sozusagen dann Widerspruch oder Verstöß gegen
den Standard. Aber das Problem ist beim Anfangsproblem, dass ich sozusagen den
Standard verlassen habe, weil ich in einem zu großen Zahlenbereich rechnen wollte oder so.
Mathias Magdowski
Würde ich so vermuten, ja. Also das, was man immer, zumindest womit man das mal so checken kann,
es gibt in allen Numerikprogrammen, die so auf dem Markt sind,
also zum Beispiel in Octave gibt es so eine Variable, die heißt EPS.
Weiß nicht, wofür genau diese.
Thomas Kahle
Epsilon. Die steht natürlich für Epsilon.
Mathias Magdowski
Epsilon, okay. Ich habe immer gedacht, das ist P für Precision oder sowas.
Nee, das ist wahrscheinlich gar nicht so eine Fehler-Fehler-Schranke.
Thomas Kahle
Ich weiß nicht, wie viele so mathematische Analysen du schon genossen hast,
aber da ist so ein Epsilon, ist diese beliebig kleine Fehler-Schranke.
Mathias Magdowski
Ja.
Thomas Kahle
Beliebig kleine, reelle Zahlen.
Mathias Magdowski
Und ich meine, wenn man die eben abfragt, sind das 2,2 mal 10 hoch minus 16 oder sowas.
Und das ist eben genau der… 2,2. 2,2, ja. 2,2 irgendwas mal 10 hoch minus 16.
Und das ist eben die Genauigkeit, die man hat, wenn man eben um 1 herum rechnet.
Und dieses 10 hoch minus 16 ist eben kleiner als das.
Und deshalb wird das von der 1 praktisch verschluckt.
Thomas Kahle
Also es gibt keine Zahlen mehr. Es gibt keine Zahlen mehr zwischen der 0 und diesem Epsilon.
Mathias Magdowski
Nein, es gibt schon noch, also ich meine, ich kann problemlos irgendwie Zahlen
hinschreiben, auch in Octave, die 10 hoch minus 20, 10 hoch minus 30,
ich weiß nicht, was da der Kleinstrecker ist, weil man den Exponenten kleiner,
aber ich meine, wenn ich das dann zu einer 1 dazu rechne.
Thomas Kahle
Dann ist es nicht mehr sichtbar.
Mathias Magdowski
Dann wird es eben verschluckt.
Ja, und deshalb widerspricht es nicht dem Standard, es ist einfach dann außerhalb des Standards.
Ja, und zum Beispiel, also ein anderes schönes Beispiel, um jetzt auf dieses
Grumim zurückzukommen, wenn man 0,1 plus 0,2 rechnet, da sollten ja irgendwie
0,3 rauskommen, wenn man dann 0,3 abzieht, dann kommen eben nicht 0 raus,
sondern zum Beispiel 5,55 mal 10 hoch minus 17.
Thomas Kahle
Aber wie kann das jetzt sein?
Mathias Magdowski
Ja, wie kann das jetzt sein? Also meine scharfe Vermutung und Schlussfolgerung
ist, dass die Zahlen, wie gesagt, ja eben nicht in einem Dezimalsystem im Computer
gespeichert sind, sondern in einem Binärsystem.
Und dadurch ist eben irgendwie die 0,1 und 0,2, die gibt es in dem Sinne eben
gar nicht so exakt, weil ich die ja versuche durch irgendwelche Zweierpotenzen,
die da so in der Nähe liegen,
irgendwie anzunähern und naja, es gibt eben keine Zweierpotenz,
die eben genau 100 macht oder 10 oder sowas, sondern die nächste ist eben irgendwo
da und deshalb entsteht dieser Fehler dann mit dem.
Thomas Kahle
Das ist das gute alte Ein-Drittel-Problem im Dezimalsystem nochmal.
Mathias Magdowski
Genau, dass man so einen Rundungsfehler hat wie, genau, ein Drittel kann ich
eben auch nicht, ist 0,33333 und dann, weiß nicht, am Ende eben eine 4 oder eine 3,
aber irgendwas fehlt immer oder 0,666667.
Sieben.
Thomas Kahle
Sind diese Rundungen eigentlich dann, die dann passieren, sind die kaufmännisch oder mathematisch?
Wie rundet der IEEE-Standort?
Mathias Magdowski
Also ich glaube, das ist das, was ich meine. Es soll immer so gerundet werden,
dass das Ergebnis eben wieder innerhalb der Rundung korrekt ist.
Thomas Kahle
Diese Freiheit muss ich da verbrateln.
Also ich habe keine konsistente Rundung, sondern ich habe eine Rundung,
die eine Garantie erfüllt hinterher für das Ergebnis.
Mathias Magdowski
So stelle ich mir das vor, ja. Und ich meine, das sind im Prinzip dann schon,
also es gibt diesen Rundungsfehler, den man sowieso mal hat.
Es gibt diesen Fehler, den schon besprochen durch diese Absorption,
wenn ich auf eine relativ große Zahl eine viel kleinere Zahl addiere,
wird die möglicherweise verschluckt. Dann gibt es noch so ein,
wenn ich jetzt das in die andere Richtung mache, gibt es so ein Fehler Auslöschung.
Also wenn ich zwei ähnlich große Zahlen subtrahiere, dann kommt da manchmal
Null raus, obwohl eben nicht genau Null rauskommen sollte.
Und das ist natürlich insbesondere dann irgendwie übel, wenn diese Differenz
im Nenner eines Bruches steht, weil man dann, also man würde eigentlich durch
was sehr Kleines teilen, durch eine Differenz ähnlich großer Zahlen,
die sehr klein wird und im Ergebnis dann eben relativ groß,
aber dann eine Division durch Null ergibt.
Und ich meine, klar, es gibt noch eigentlich das, was man auch so total naiv
erwarten würde, einfach irgendwann ist mein Zahlenbereich eben nach oben vorbei
und dann gibt es so einen Überlauf und dann muss man eben irgendwie schauen,
wie man mit dem Überlauf umgeht und genauso gibt es auch so einen Unterlauf.
Also wenn ich von einer sehr kleinen Zahl eine noch kleinere Zahl subtrahiere
und nochmal subtrahiere, also dass ich mich immer näher an die Null annähere,
irgendwann ist die Zahl eben zu klein, die ich darstellen kann.
Oder wenn ich nehme was und teile durch 10 und nochmal durch 10 und nochmal
durch 10 und irgendwann bin ich eben aus dem darstellbaren Bereich raus.
Das sind eigentlich, würde ich sagen, so zusammengefasst die vier Fehler,
die es geben kann. Diese Rundung, Absorption, Auslöschung und Unterlauf, Überlauf.
Thomas Kahle
Und sag mal, wie kannst du jetzt zu diesem Preisschild kommen?
Also das ist für mich immer noch so ein Rätsel. Also da steht einfach ein Preis
drauf und der soll offensichtlich 279,99 Euro sein,
aber schon der Originalpreis, also es hat nichts mit der Berechnung des Rabatts zu tun, scheint mir.
Schon der Originalpreis hat eben diese Eigenschaft, dass er eben nicht 99 Cent,
sondern 99,000001 Cent.
Mathias Magdowski
Genau, also weil wieder es ist dargestellt durch eine Zweierpotenz und durch
die Zweierpotenz oder durch die Darstellung im Binärsystem kann man eben nicht
exakt die 279,99 darstellen,
sondern da ist hinten immer noch so ein Beschwänzchen an irgendwie 0,00000 irgendwas dran.
Thomas Kahle
Also der Implementierungsfehler ist, dass vor der Ausgabe eines Preises grundsätzlich
auf zwei Stellen zu runden ist.
Mathias Magdowski
Genau, also da ist so ein Numb-to-String mit viel zu vielen Nachkommastellen
oder irgendwie nicht auf, ja.
Ich glaube, dass wir so im normalen Leben auch als IngenieurInnen irgendwie
relativ wenig von dieser Problematik merken, weil die ganzen Programme, die wir benutzen,
also zumindest eben so was wie Octave, Matlab, Python, dass die schon ziemlich
schlau darin sind, irgendwie solche Fehler vor einem zu verstecken oder irgendwie
zu verbergen, zu verheimlichen. Und man sowas eben.
Erstmal nur dann sieht, wenn man selber sich in C++ irgendwie irgendwas programmiert
oder eben auf einem Mikrocontroller oder eben irgendwelche andere Drittsoftware benutzt.
Also ich simuliere ganz gerne mal Schaltungen im Netzwerksimulator LTSpice zum
Beispiel und da ist das auch so.
So, wenn man zum Beispiel mit, wie vorhin angesprochen, komplexen Zahlen rechnet
und da kommt ein komplexer Zeiger raus, eine komplexe Zahl, dann hat die ja
einen Betrag und einen Phasenwinkel.
Ich kann sie darstellen als realen und imaginären Teil oder eben auch als Betrag und Phasenwinkel.
Und der Phasenwinkel, wenn ich eine rein reelle Zahl habe, die ich dann irgendwie
in diesem komplexen Zahlenformat darstelle, ist ja der Phasenwinkel 0.
Und dann kommt das mal ganz gern vor, wenn man dann so ein Diagramm plottet,
dass da eben nicht eine Linie bei 0 ist,
sondern dass da eine Linie ist, die rauscht und zittert und schittert wie verrückt
und die ist dann eben mal plus 10 hoch minus 16 Grad,
minus irgendwas 10 hoch minus 16 Grad.
Also da ist einfach ein numerischer Rundungsfehler drin, wo dann,
naja, die Achsenskalierung des Diagramms eben fehlschlägt und einem versucht diese,
was weiß ich, Billiardstel, Billionstel Grad irgendwie anzuzeigen,
noch aufzulösen, was dann an der Stelle natürlich…,
Wahnsinnig zielführend ist und ich glaube, also das ist hier genau das gleiche
Problem hier. Ja und das ist einfach ein Darstellungsproblem.
Also man hätte auf zwei Nachkommastellen in Cent runden sollen und das damit anzeigen sollen.
Thomas Kahle
Aber in irgendeiner Datenbank wurde der Preis auch nicht von einem Menschen
eingetragen, sondern auch anscheinend schon irgendwie berechnet.
Also es ist auch interessant, dass der Preis 279,99, dass der,
wie wurde der, warum wurde der berechnet und warum sind dabei so kleine Zahlen aufgedacht?
Mathias Magdowski
Ja, ich glaube, das Problem ist, also wenn jetzt diese Datenbank eben nicht,
wie angesprochen, mit so einer Fixkomma-Arithmetik arbeitet,
sondern das als Gleitkommazahl speichert, ich meine, dann kann ich eben nicht
279,99 exakt, also wenn ich 279,99 exakt dort eingebe.
Thomas Kahle
Würde es nicht wieder rauskommen.
Mathias Magdowski
Genau.
Thomas Kahle
Schon allein das Auslesen dieses Feldes würde.
Mathias Magdowski
Genau, also weil sobald ich diese Zahl vom Dezimalsystem in diese Gleitkommazahl
im Binärsystem umwandle,
entsteht dieser praktisch Rundungsfehler, dass da diese 0,000001 hinten entstehen.
Also wahrscheinlich ist das an der Stelle keine wahnsinnig schlaue Idee,
das eben in Gleitkommazahlen zu speichern und dann auch noch irgendwie diesen
Fehler zu machen bei der Ausgabe.
Und ja klar, und dann, dass es eben niemandem aufgefallen ist,
weil ganz offensichtlich diese Schilder massiv automatisiert erzeugt werden
und dann selbst bei der Person, die das irgendwie ausgehangen hat im Markt,
eben es nicht klick gemacht hat.
Thomas Kahle
Genau, also es ist ein Foto und man erkennt sogar im Hintergrund sogar noch,
dass dort, dass es im echten Markt zum Einsatz kommt.
Also hinten rechts ist auch so ein Regal zu erkennen oder auch irgendwie so
ein Hosenbein von der Person, die da gerade noch im Hintergrund vorbeigeht.
Also es ist wirklich im Einsatz. Das Schild.
Mathias Magdowski
Ja, ist natürlich immer die Frage bei solchen Schildern, wie weit das nicht
vielleicht auch irgendjemand gefakt hat, aber es sieht mir doch relativ realistisch aus.
Und ich meine, wir kennen alle solche Schilder, wo,
Auch so einen ähnlichen Rabatt und dann ist aber der Rabatt irgendwie positiv
und der neue Preis ist noch teurer als der alte Preis.
Thomas Kahle
1,5 Euro, 3, nur 16.
Mathias Magdowski
Genau.
Thomas Kahle
Irgendwie diese Art von Rabatten.
Mathias Magdowski
Oder diese Art von Rabatten, ja. Also ich glaube, das kommt doch häufiger mal
vor, dass so Preisschilder irgendwie nicht so ganz der Realität entsprechen.
Ich weiß ja gar nicht, wie das ist so mit zehntel Cent. Also an Tankstellen
hat man ja auch das Problem, aber ich glaube, da wird dann einfach auch immer gerundet.
Thomas Kahle
Es gibt doch so einen Film. Gibt es nicht irgendwie einen Film,
wo irgendwelche Computerhacker die ganzen Rundungsfehler bei der Bank auf ihr
Konto überweisen und dann damit reich werden?
Mathias Magdowski
Das kann gut möglich sein. Also es gibt ja auch auf jeden Fall Länder in Europa,
die den 1 Cent und 2 Cent überhaupt gar nicht ausgegeben haben und benutzen,
sondern generell immer auf 5 Cent runden.
Wenn man auch im Supermarkt einkauft. Und ich kann mich auch noch erinnern,
dass ich bei irgendeiner Informationsveranstaltung zur D-Mark in Euro-Umstellung
in meiner Bank war und dann der Bankberater gesagt hat, es ist ein todsicheren Weg,
sein Vermögen sozusagen im Rahmen der Euro-D-Mark-Euro-Umstellung zu verdoppeln.
Man muss einfach ein Konto anlegen mit einem Pfennig drauf und das wird dann
bei der Umstellung eben gerundet in einen Cent und da der Cent ja ungefähr doppelt
so viel wert ist, wie der Pfennig, vorher hat man sein Vermögen dann verdoppelt an der Stelle.
Also nicht, auch nicht sehr praxisrelevant, weil man müsste sehr viele Konten anlegen.
Thomas Kahle
Ja, das kann nervig sein. Ich glaube, das ist, also ich stelle mir das nervig
vor, so viele Konten zu haben.
Mathias Magdowski
Definitiv, ja. Es gibt noch ein, glaube ich, ganz nettes Buch und Skript,
auf das wir verweisen können, Gleitkomma-Arithmetik auf dem Prüfstand von Siegfried Rump.
Das ist, glaube ich, auch ganz nett, wenn man mal noch irgendwie ein bisschen
tiefer und in die Thematik einsteigen will.
Und also wo das auch mal in der Hinsicht ein bisschen tatsächlich in meiner
Praxis aufgetaucht ist und wo ich glaube ich vor zwei Jahren mal mit einem Kollegen
von der Ostfalia Hochschule ein Paper darüber geschrieben habe,
ist, wir haben ein Messgerät, auch bei uns herumzustehen, einen Impedanzanalysator.
Mit dem kann man eben Impedanzen messen. Impedanz ist Verhältnis von Spannung und Strom.
Also sowas wie ein Widerstand, bloß eben als komplexe Zahl und dann in Abhängigkeit von der Frequenz.
Und dieser Impedanzanalysator, der ist auch nicht ganz günstig.
Also der kostet schon, kann man schon auch ein gutes Mittelklasse-Auto von kaufen, sage ich mal so.
Und der im Normalfall speichert ja eben diese Impedanzen, die eine komplexe
Zahl sind, einfach als Betrag und Phasenwinkel.
Und der Betrag ist dann eben irgendwie eine Gleitkommazahl und der Phasenwickel
ist eine Gleitkommazahl, alles super gut.
Und dann kann man eben sehr kleine und sehr große Impedanzen ganz wunderbar
damit darstellen. Hat genau diese Vorteile, die wir gerade besprochen haben.
Und dann kann man den aber auch so umstellen.
Dass der die Ergebnisse nicht direkt als eine Impedanz speichert,
sondern als so ein Streuparameter.
Und Streuparameter sind eigentlich was, was man mit einem anderen Messgerät
in der Elektrotechnik misst, mit Netzwerkanalysatoren oder Vektornetzwerkanalysatoren.
Und um jetzt irgendwie Ergebnisse besser von dem einen Messgerät mit dem anderen
Messgerät vergleichen zu können, da haben die da auch sowas implementiert.
Also man misst mit dem Impedanzanalysator, tut aber so, wie wenn das eigentlich
Ergebnisse sind von so einem Netzwerkanalysator.
Und die Umrechnung ist eben einmal, wenn man von diesen Impedanzen umrechnet
in Streuparameter, hat man einmal sowas wie eine Differenz von Impedanzen geteilt durch eine Summe.
Ja, das ist typischerweise unkritisch, weil okay, dann wird die Differenz vielleicht
klein, aber die Summe wird irgendwie immer demgegenüber groß. Also kleiner Fehler.
Also genau das ist da dann aufgetaucht. Also ich habe bei uns hier Messungen
gemacht, kam irgendwas bei raus. Der Kollege an der Osfalia hat Messungen gemacht.
Da kam prinzipiell genau das Gleiche raus. Wir haben das nur jeweils in einem
anderen Datenformat abgespeichert und irgendwie am Ende ausgewertet.
Und die Kurven sahen dann, naja, nicht komplett unterschiedlich aus,
aber da gab es auf jeden Fall eklatante Unterschiede.
Und das hat eine ganze Weile dann gedauert, bis wir dem auf die Stiche gekommen
sind, dass das eben kein Messfehler ist, dass das Messgerät nicht kaputt ist,
sondern dass das wirklich einfach nur eine Frage ist,
in welchem Format speichert man die Daten da ab und mit welcher Genauigkeit
werden die gespeichert und das Problem ist,
dass die dann, dass der Hersteller dieses doch durchaus sehr teuren Messgerät,
das sich nicht wahnsinnig klug dabei eingestellt hat, sich da irgendwie ein
schlaues Zahlenformat zu speichern, weil die nämlich im Prinzip wirklich einfach
sowas wie so ein Festkomma oder eben das Problem haben,
also wenn dieser Streuparameter, den man da ausrechnet, wenn der eben nahe 1 ist,
Ja, dann habe ich ja 0,999999999999999999999999999999999999.
Wie viele 9 nach dem Komma nehme ich dann mit? Und eigentlich wäre es viel besser,
von dem Streumparameter eben eine 1 abzuziehen, um diese, was du gesagt hast,
diese gute Genauigkeit, diese immer
bessere, immer feinere Genauigkeit der Gleitkommazahlen um die 0 zu haben.
Und dadurch, dass aber, na ja, eigentlich der Streumparameter so um 1 rumschwankt,
habe ich dann so diese sehr grobe Genauigkeit um die 1 ringsrum,
die dann sehr stark davon abhängt, wie viele Nachkommastellen packe ich da an diese Mantisse ran.
Thomas Kahle
Also eigentlich hatten wir erst die Gleitkomma-Arithmetik erfunden,
um eine gute Abdeckung eines großen Zahlenbereichs zu haben,
aber jetzt kriegen wir eben nicht eine gute Abdeckung um eine beliebige Zahl
herum, sondern nur um die 0 herum.
Also hat man jetzt wieder so eine Modellabhängigkeit, also dass man noch was verbessern kann,
wenn man weiß, die Zahlen, die ich gut abspeichern will, sind die,
die um die 1 herumliegen, dann könnte ich da noch die 1 abziehen und das Datenformat
wieder ändern, um es anzupassen an die Situation. tun.
Mathias Magdowski
Genau, genau. Also da ist, ne und das ist also bei den Impedanzen,
da passt das auf einmal, weil,
wenn die eben sehr klein sind, dann habe ich diese Supergenauigkeit um 0,
wenn die sehr groß sind, dann werden die eben sehr groß, also kein Problem,
aber bei diesen Streuparameter ist es so, der eigentlich kann ja nicht größer werden als 1,
ja, weil das wäre irgendwie unphysikalisch, wenn dann mehr zurückreflektiert
wird von einer passiven Last, als ich eben darauf sende, aber der,
geht sozusagen immer dichter an die 1 ran, ne, also 0,99, 0,999,
0,999 und Und eigentlich ist nur die Frage, wie viele Neunen kommen da hinter
dem Komma und wie dicht bin ich an der Eins dran?
Und genau das kann jetzt eine normale, beliebige Gleitkommazahl jetzt nicht gut darstellen.
Thomas Kahle
Also die Frage, die sich jetzt glaube ich alle stellen, ist schon eine Mars-Mission
abgestürzt wegen solches Problem?
Mathias Magdowski
Es ist mal irgendeine Ariane-Rakete, soweit ich weiß, abgestürzt,
weil es da irgendeinen Pufferüberlauf gab.
Also es ist glaube ich, um wieder auf das Einleitenthema zurückzukommen,
es sind glaube ich mal irgendwelche Raumsonden abgestürzt, weil Leute vergessen
haben, Fuß in Meter und so umzubauen.
Thomas Kahle
Ja, das war ja unsere letzte, in unserer letzten Folge. Genau, ich denke ja.
Mathias Magdowski
Meines Erachtens ist es auch mal, wir können das gerne nochmal recherchieren,
habe ich mich jetzt im Vorfeld nicht beschäftigt, meines Erachtens ist es auch
mal eine Rakete abgestürzt,
weil sie einfach eine Steuerungseinheit aus einer alten Rakete genommen haben,
die neue Rakete aber höher, schneller, besser weiterflog und es dann einfach
zu dem besprochenen Überlauf kam und der dann nicht vernünftig abgefangen wurde
oder einfach eben nicht genügend Speicher da war.
Ja, und ich meine, also das, was ja bei meiner praktischen Wenn man in der praktischen
Rechnung immer nochmal so ganz gern rauskommt, ist dann, dass da Inf rauskommt,
also für Infinity, für Unnötigkeit oder Minus Inf oder NAN für Not a Number
und dann weiß man schon, okay, da ist jetzt irgendwas schief.
Thomas Kahle
Diese ganzen Sachen sind auch spezifiziert, sind auch Teil des Standards.
Mathias Magdowski
Und die sind auch Teil des Standards, ja. Und ich glaube, da steckt eben auch
so ein bisschen Dings drin, Regelwerk in, wann werden diese Fehler gesetzt und
wie geht man eben danach um.
Ja, also in der praktischen Rechnung im alltäglichen Leben weiß man schon,
okay, wenn das da rauskommt, irgendwo vorher muss ich dann mal schauen,
bis wo das Ergebnis dann noch stimmte und wann es dann eben nicht mehr stimmte.
Und also womit man, wenn man jetzt sagt, ach naja, das ist jetzt irgendwie ein
super akademisches Thema und also dieses 1 plus minus 10 hoch minus 16 Problemen,
also wo sowas auch jetzt noch relativ gut und schnell auftaucht und wo man es
gut mit reproduzieren kann,
ist, wenn man einfach so ein bisschen Bruchrechnung macht in Octave, in MATLAB.
Ja, und immer so Sachen hat wie, also ich nehme n plus 1 durch n,
ja, also wenn wir jetzt sozusagen so im Kopf rechnen, meinetwegen mit einem
Beispiel 11 Zehntel, ja, so sind irgendwie 1,1, jetzt wissen wir schon,
1,1 kann man eigentlich nicht so wirklich darstellen, da kommt irgendwie was
anderes komisches raus.
Jetzt ziehe ich von den 1,1 eben 1 ab, dann sollte also 11 Zehntel minus 1 macht
1 Zehntel oder 0,1 und jetzt rechne ich das Ganze wieder mal 10,
dann sollte sozusagen wieder 1 rauskommen und jetzt wissen wir ja,
okay, um 1 rum ist die Genauigkeit nicht so super gut und sowas,
jetzt ziehe ich sozusagen wieder eine 1 ab, um diesen kleinen Fehler da auch rauszubekommen.
Und da kann man nahezu beliebige Zahlen einsetzen in dieses n plus 1 durch n
minus 1 mal n nochmal minus 1.
Da sollte ideal 0 rauskommen, kommt aber relativ selten 0 raus,
sondern immer irgendwas ein paar plus und ein paar minus 10 hoch minus 16.
Meistens mit Vielfachen von diesem EPS, von diesem Epsilon.
Thomas Kahle
Ja, also man hat das Problem nicht gelöst, sondern man hat das Problem nur standardisiert.
Das ist das Problem des Rechnens mit reellen Zahlen.
Ich kann auch mal irgendwann, also das kann ich heute nicht mehr erzählen,
da muss ich mich auch noch ein bisschen drauf vorbereiten, es gibt auch so ein
Berechenbarkeitsmodell, also das ist jetzt natürlich wieder ein Gedankenexperiment,
ein theoretisches Modell von einem Computer, der wirklich mit reellen Zahlen rechnen kann.
Also einfach, wo die Grundspeichereinheit, die speichert eine reelle Zahl ab, eine beliebige.
Und die Rechenoperationen sind auch alle implementiert. Und dann kann man aber
trotzdem immer noch da für Komplexitätstheorie machen und sich überlegen,
was das Ding berechnen kann.
Das ist wie so eine Variante der Turing-Maschine, die kontinuierlich ist.
Statt sozusagen in ein diskretes Band kann die eben reelle Zahlen abspeichern.
Aber da erzähle ich mal von anders drüber.
Mathias Magdowski
Genau und mit dieser Standardisierung, ich meine wir sagen auch in der Elektrotechnik
gibt es ja auch super viele Standards um irgendwelche Messungen zu machen,
da gibt es auch so den schönen Spruch, also wenn alle nach dem Standard messen,
messen alle falsch, aber es messen wegen es alle gleich falsch,
weil alle dann den gleichen Fehler machen und ich glaube das ist hier genau
die gleiche Kiste, also früher war es eben so, man hat die Rechnung unterschiedlicher Computer gegeben,
die haben im Zweifel alle unterschiedliche Ergebnisse rausgerechnet,
man wusste gar nicht so was richtig war, jetzt rechnen eben immerhin alle gleich falsch.
Also das ist ja wohl auch der Legende nach ein sehr praktisches Problem hier
bei so diesen ersten Raumfahrtmissionen der USA gewesen mit,
wie hieß denn der erste, den sie wirklich in eine Umlaufbahn geschossen haben?
Alan Shepard, Gus Grissom, John Glenn, John Glenn?
Und das ist ja, also da gibt es ja diesen The Hidden Figures,
diesen halb dokumentarischen Film drüber, der auch auf so schon sehr wahren
Begebenheiten glaube ich beruht und dass ja dann die NASA so einen der ersten
größeren IBM Mainframe Computer hatte und dass der sich auch unsicher war oder sagen wir mal,
dass es vielleicht auch Probleme in der Programmierung gab oder in der Interpretation der Ergebnisse.
Und den einen Tag hat der Computer so gerechnet und am nächsten Tag der Computer
so und dann hat der John Glenn wohl gesagt,
naja, also wenn ihr euch nicht sicher seid, wie euer Computer da rechnet,
also dann setze ich mich hier nicht auf so eine Rakete und so eine Kapsel und
wer weiß, ob ich dann aus der Erd-Umlaufbahn rausfliege oder ob ich wieder im
richtigen Moment abgebremst bekomme, dass ich hier doch wieder irgendwo lande
und hat dann wohl da drauf bestanden und es ist der Ausspruch überliefert get
the girls to check the numbers,
also diese menschlichen Computer, die afroamerikanischen Damen,
die da für die NASA tätig waren, doch bitte mal zu beauftragen,
die Rechnung des Computers zu überprüfen.
Also dann kam wohl was Konsistentes bei raus und dann ist er natürlich dementsprechend auch geflogen.
Aber das ist also heutzutage unsichtbar wird der Fehler, wenn sich alle daran gewöhnt haben.
Thomas Kahle
Wollen wir das als Schlusswort nehmen? Ein sehr schönes Schlusswort.
Gut, dann danke Matthias. Sehr gern. Und ich sag jetzt einfach mal bis zum nächsten Mal.
Mathias Magdowski
Ciao.
Thomas Kahle
Für euch auf diesem Kanal und für Matthias auch auf diesem Kanal. Tschüss.